梯度下降 是深度学习中最常用的一种优化算法 ,是深度学习绕不开的前置知识,因此,本文将介绍梯度下降的思想与数学实现 ,并且简单介绍一些梯度下降的变体算法。
首先,我们要弄清楚梯度下降到底是用来干什么的,为什么梯度下降在深度学习中有这么广泛的应用。机器学习与深度学习算法本质上是一类依赖数据驱动的算法,在这类算法中常常会引入一个损失函数 ,例如线性回归 中的平方误差损失函数(MSE)。而引入损失函数的算法的训练本质上就是求解损失函数最小值的过程 。这个时候我们就会发现,我们需要一种算法来实现求解损失函数最小值这个需求,而用于求解函数最值 的这一类算法,就被称为优化算法 。
上面说到,所谓优化算法,其实就是求函数最值的算法 。那么这样一类算法应该如何实现呢,答案就是搜索 ,可以说优化算法本质上就是搜索的艺术。我们假设一个简单的情况,例如一个定义域在[ 0 , 1 ] [0,1] [ 0 , 1 ] x x x y y y y y y 暴力搜索 。没有规则,没有章法,只要我搜索的次数足够多,我就一定能找到最值。
暴力搜索虽然简单,但是其缺点也很明显,对于复杂度过高的问题,例如一系列NP-hard问题,在现代计算机的算力下暴力搜索是无法在可以接受的时间内完成计算的。而即使是一般复杂度的问题,暴力搜索的效率也十分优先,收敛速度很慢,在时间与算力都极度昂贵的人工智能领域,这显然是不能接受的,那我们应该如何改进暴力搜索呢。既然暴力搜索是完全随机, 没有规则的搜索,那我们只要给其加入一个规则 ,告诉算法应该要往哪个方向搜索 就好了,这也是一众优化算法关心的事情。
铺垫做完了,现在让我们回到梯度下降。梯度下降算法给搜索加了什么规则呢,我们直观的理解一下梯度下降的搜索策略,先从一元的情况看起,如下图
梯度下降算法的做法是,先随机生成一个初始值,然后在初始值的位置上寻找一个下降速度最快的方向 ,往这个方向前进一段距离,再停下来看看,重新寻找下降速度最快的方向,如此往复,就像下山 一样。
当然,一元的情况只有正负两个方向,我们来看看多元的情况,如下图
上图是一个二元函数的等高线图,红点处是其真实最小值,可以看到二元函数的情况其方向选择就复杂了起来,但是总体思想还是不变的。
在了解了梯度下降的思想之后,我们发现梯度下降的核心就在于找下降速度最快的方向 ,并且我们要用数学工具来表达,下面我们就来看看梯度下降的具体数学实现。
首先我们来讲一下梯度 ,这是我们用于表达下降速度最快的方向的秘密武器,其实在高数课本中就有提到梯度,但是其存在感并不强,这里我们先来回顾一下。梯度大家可能不记得了,偏导数 大家应该还是有印象的吧。对于一个二元函数f ( x , y ) f(x,y) f ( x , y ) ∂ f ∂ x \frac{\partial f}{\partial x} ∂ x ∂ f ∂ f ∂ y \frac{\partial f}{\partial y} ∂ y ∂ f 梯度 就是由这两个偏导数 组成的二维向量 ( ∂ f ∂ x , ∂ f ∂ y ) T (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})^T ( ∂ x ∂ f , ∂ y ∂ f ) T ∇ f ( x , y ) \nabla f(x,y) ∇ f ( x , y ) g r a d f ( x , y ) \mathrm{grad} f(x,y) g r a d f ( x , y ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 )
∇ f ( x 0 , y 0 ) = ( ∂ f ∂ x ∣ x = x 0 , ∂ f ∂ y ∣ y = y 0 ) T \nabla f(x_0,y_0) = \left( \left. \frac{\partial f}{\partial x} \right|_{x=x_0}, \left. \frac{\partial f}{\partial y} \right|_{y=y_0} \right)^T
∇ f ( x 0 , y 0 ) = ( ∂ x ∂ f ∣ ∣ ∣ ∣ ∣ x = x 0 , ∂ y ∂ f ∣ ∣ ∣ ∣ ∣ y = y 0 ) T
而∇ f ( x 0 , y 0 ) \nabla f(x_0,y_0) ∇ f ( x 0 , y 0 ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) ( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 )
− ∇ f ( x 0 , y 0 ) = − ( ∂ f ∂ x ∣ x = x 0 , ∂ f ∂ y ∣ y = y 0 ) T - \nabla f(x_0,y_0) = - \left( \left. \frac{\partial f}{\partial x} \right|_{x=x_0}, \left. \frac{\partial f}{\partial y} \right|_{y=y_0} \right)^T
− ∇ f ( x 0 , y 0 ) = − ( ∂ x ∂ f ∣ ∣ ∣ ∣ ∣ x = x 0 , ∂ y ∂ f ∣ ∣ ∣ ∣ ∣ y = y 0 ) T
最后,我们来给出更一般的多元函数的梯度表达式。对于多元函数f ( x 1 , x 2 , ⋯ , x n ) f(x_1,x_2,\cdots,x_n) f ( x 1 , x 2 , ⋯ , x n ) ( x 10 , x 20 , ⋯ , x n 0 ) (x_{10},x_{20},\cdots,x_{n0}) ( x 1 0 , x 2 0 , ⋯ , x n 0 )
∇ f ( x 1 , x 2 , ⋯ , x n ) = ( ∂ f ∂ x 1 ∣ x 1 = x 10 , ∂ f ∂ x 2 ∣ x 2 = x 20 , ⋯ , ∂ f ∂ x n ∣ x n = x n 0 ) T \nabla f(x_1,x_2,\cdots,x_n) = \left( \left. \frac{\partial f}{\partial x_1} \right|_{x_1=x_{10}}, \left. \frac{\partial f}{\partial x_2} \right|_{x_2=x_{20}}, \cdots, \left. \frac{\partial f}{\partial x_n} \right|_{x_n=x_{n0}} \right)^T
∇ f ( x 1 , x 2 , ⋯ , x n ) = ( ∂ x 1 ∂ f ∣ ∣ ∣ ∣ ∣ x 1 = x 1 0 , ∂ x 2 ∂ f ∣ ∣ ∣ ∣ ∣ x 2 = x 2 0 , ⋯ , ∂ x n ∂ f ∣ ∣ ∣ ∣ ∣ x n = x n 0 ) T
现在就剩下最后一个问题,参数的更新,也就是下降一步,在数学上是如何表达的。首先是一元的情况,这个很简单,从x 0 x_0 x 0 x 1 x_1 x 1 − ∂ f ∂ x ∣ x = x 0 - \left. \frac{\partial f}{\partial x} \right|_{x=x_0} − ∂ x ∂ f ∣ ∣ ∣ ∣ x = x 0 x 1 = x 0 + ( − ∂ f ∂ x ∣ x = x 0 ) x_1 = x_0 + (- \left. \frac{\partial f}{\partial x} \right|_{x=x_0}) x 1 = x 0 + ( − ∂ x ∂ f ∣ ∣ ∣ ∣ x = x 0 ) α \alpha α
x 1 = x 0 − α ∂ f ∂ x ∣ x = x 0 x_1 = x_0 - \alpha \left. \frac{\partial f}{\partial x} \right|_{x=x_0}
x 1 = x 0 − α ∂ x ∂ f ∣ ∣ ∣ ∣ ∣ x = x 0
然后是二元的情况,这个要稍微复杂一点,从( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) − ( ∂ f ∂ x ∣ x = x 0 , ∂ f ∂ y ∣ y = y 0 ) T - \left( \left. \frac{\partial f}{\partial x} \right|_{x=x_0}, \left. \frac{\partial f}{\partial y} \right|_{y=y_0} \right)^T − ( ∂ x ∂ f ∣ ∣ ∣ ∣ x = x 0 , ∂ y ∂ f ∣ ∣ ∣ ∣ y = y 0 ) T ( x 1 , y 1 ) (x_1,y_1) ( x 1 , y 1 ) x 0 x_0 x 0 − ∂ f ∂ x ∣ x = x 0 - \left. \frac{\partial f}{\partial x} \right|_{x=x_0} − ∂ x ∂ f ∣ ∣ ∣ ∣ x = x 0 y 0 y_0 y 0 − ∂ f ∂ y ∣ y = y 0 - \left. \frac{\partial f}{\partial y} \right|_{y=y_0} − ∂ y ∂ f ∣ ∣ ∣ ∣ y = y 0 α \alpha α
x 1 = x 0 − α ∂ f ∂ x ∣ x = x 0 y 1 = y 0 − α ∂ f ∂ y ∣ y = y 0 x_1 = x_0 - \alpha \left. \frac{\partial f}{\partial x} \right|_{x=x_0} \\
y_1 = y_0 - \alpha \left. \frac{\partial f}{\partial y} \right|_{y=y_0}
x 1 = x 0 − α ∂ x ∂ f ∣ ∣ ∣ ∣ ∣ x = x 0 y 1 = y 0 − α ∂ y ∂ f ∣ ∣ ∣ ∣ ∣ y = y 0
同理,对于一般的多元函数f ( x 1 , x 2 , ⋯ , x n ) f(x_1,x_2,\cdots,x_n) f ( x 1 , x 2 , ⋯ , x n ) ( x 1 m , x 2 m , ⋯ , x n m ) (x_{1m},x_{2m},\cdots,x_{nm}) ( x 1 m , x 2 m , ⋯ , x n m ) ( x 1 , m + 1 , x 2 , m + 1 , ⋯ , x n , m + 1 ) (x_{1,m+1},x_{2,m+1},\cdots,x_{n,m+1}) ( x 1 , m + 1 , x 2 , m + 1 , ⋯ , x n , m + 1 )
x 1 , m + 1 = x 1 m − α ∂ f ∂ x 1 ∣ x 1 = x 1 m x 2 , m + 1 = x 2 m − α ∂ f ∂ x 2 ∣ x 2 = x 2 m ⋯ x n , m + 1 = x n m − α ∂ f ∂ x n ∣ x n = x n m x_{1,m+1} = x_{1m} - \alpha \left. \frac{\partial f}{\partial x_1} \right|_{x_1=x_{1m}} \\
x_{2,m+1} = x_{2m} - \alpha \left. \frac{\partial f}{\partial x_2} \right|_{x_2=x_{2m}} \\
\cdots \\
x_{n,m+1} = x_{nm} - \alpha \left. \frac{\partial f}{\partial x_n} \right|_{x_n=x_{nm}}
x 1 , m + 1 = x 1 m − α ∂ x 1 ∂ f ∣ ∣ ∣ ∣ ∣ x 1 = x 1 m x 2 , m + 1 = x 2 m − α ∂ x 2 ∂ f ∣ ∣ ∣ ∣ ∣ x 2 = x 2 m ⋯ x n , m + 1 = x n m − α ∂ x n ∂ f ∣ ∣ ∣ ∣ ∣ x n = x n m
记x = ( x 1 , x 2 , ⋯ , x n ) T \boldsymbol{x} = (x_1,x_2,\cdots,x_n)^T x = ( x 1 , x 2 , ⋯ , x n ) T x m = ( x 1 m , x 2 m , ⋯ , x n m ) T \boldsymbol{x}_m = (x_{1m},x_{2m},\cdots,x_{nm})^T x m = ( x 1 m , x 2 m , ⋯ , x n m ) T x m + 1 = ( x 1 , m + 1 , x 2 , m + 1 , ⋯ , x n , m + 1 ) T \boldsymbol{x}_{m+1} = (x_{1,m+1},x_{2,m+1},\cdots,x_{n,m+1})^T x m + 1 = ( x 1 , m + 1 , x 2 , m + 1 , ⋯ , x n , m + 1 ) T
x m + 1 = x m − α ∇ f ( x 1 m , x 2 m , ⋯ , x n m ) = x m − α ∂ f ∂ x ∣ x = x m \boldsymbol{x}_{m+1} = \boldsymbol{x}_m - \alpha \nabla f(x_{1m},x_{2m},\cdots,x_{nm}) = \boldsymbol{x}_m - \alpha \left. \frac{\partial f}{\partial \boldsymbol{x}} \right|_{\boldsymbol{x}=\boldsymbol{x}_m}
x m + 1 = x m − α ∇ f ( x 1 m , x 2 m , ⋯ , x n m ) = x m − α ∂ x ∂ f ∣ ∣ ∣ ∣ ∣ x = x m
其中的∂ f ∂ x ∣ x = x m \left. \frac{\partial f}{\partial \boldsymbol{x}} \right|_{\boldsymbol{x}=\boldsymbol{x}_m} ∂ x ∂ f ∣ ∣ ∣ ∣ x = x m f f f x \boldsymbol{x} x
∂ f ∂ x ∣ x = x m = ( ∂ f ∂ x 1 ∣ x 1 = x 1 m , ∂ f ∂ x 2 ∣ x 2 = x 2 m , ⋯ , ∂ f ∂ x n ∣ x n = x n m ) T \left. \frac{\partial f}{\partial \boldsymbol{x}} \right|_{\boldsymbol{x}=\boldsymbol{x}_m} = \left( \left. \frac{\partial f}{\partial x_1} \right|_{x_1=x_{1m}}, \left. \frac{\partial f}{\partial x_2} \right|_{x_2=x_{2m}}, \cdots, \left. \frac{\partial f}{\partial x_n} \right|_{x_n=x_{nm}} \right)^T
∂ x ∂ f ∣ ∣ ∣ ∣ ∣ x = x m = ( ∂ x 1 ∂ f ∣ ∣ ∣ ∣ ∣ x 1 = x 1 m , ∂ x 2 ∂ f ∣ ∣ ∣ ∣ ∣ x 2 = x 2 m , ⋯ , ∂ x n ∂ f ∣ ∣ ∣ ∣ ∣ x n = x n m ) T
至此,我们完成了梯度下降算法核心部分的介绍,最后我们来看完整的梯度下降算法流程
输入:损失函数L ( w ) L(\boldsymbol{w}) L ( w ) m m m α \alpha α
输出:最后一轮的迭代结果w m \boldsymbol{w}_m w m L ( w ) L(\boldsymbol{w}) L ( w ) w m i n \boldsymbol{w}_{min} w m i n
(1) 随机选取初始值w 0 \boldsymbol{w}_0 w 0 i = 1 i=1 i = 1
(2) 计算梯度∂ L ∂ w ∣ w = w i − 1 \left. \frac{\partial L}{\partial \boldsymbol{w}} \right|_{\boldsymbol{w}=\boldsymbol{w}_{i-1}} ∂ w ∂ L ∣ ∣ ∣ w = w i − 1
(3) 更新参数w i = w i − 1 − α ∂ L ∂ w ∣ w = w i − 1 \boldsymbol{w}_i = \boldsymbol{w}_{i-1} - \alpha \left. \frac{\partial L}{\partial \boldsymbol{w}} \right|_{\boldsymbol{w}=\boldsymbol{w}_{i-1}} w i = w i − 1 − α ∂ w ∂ L ∣ ∣ ∣ w = w i − 1
(4) 若i = m i=m i = m i = i + 1 i = i + 1 i = i + 1
至此我们已经了解了梯度下降算法,但是我们学习梯度下降本质上还是要为深度学习中的各种算法服务的,光说不练假把式,我们就以最简单的线性回归为例,结合代码实现,看看梯度下降在实际的算法中是如何发挥作用的,对线性回归不了解的可以移步本站的线性回归blog 。为了更好的关注算法细节,这里我们不会使用任何机器学习算法库,而是只是用numpy,进行算法的从零实现。
注:numpy是一个科学计算库,其对矩阵运算有着很好的支持,对于从零实现算法是非常合适的选择。
首先,我们先来做一点准备工作,导入必要的依赖库,除了numpy,我们还会导入matplotlib用于实现一部分可视化的需求,并且由于后续代码涉及随机生成,因此我们会设定随机种子,运行环境为jupyter notebook
1 2 3 4 5 6 7 import matplotlib.pyplot as pltimport numpy as npimport warningswarnings.filterwarnings("ignore" ) np.random.seed(1008 )
为了方便我们验证算法的效果,这里我们选择使用自己生成的数据集,生成思路与代码详解可见本站线性回归blog 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def synthetic_data (n, w ): w = np.array(w) X = np.random.uniform(-1 , 1 , [n, np.size(w)-1 ]) I = np.ones((n, 1 )) X_hat = np.hstack((I, X)) y = X_hat @ w.T y = y.reshape(n, 1 ) y = y + np.random.randn(n, 1 ) return X, y
1 2 3 4 5 n = 1008 w = [8 , 3 , -4 ] X, y = synthetic_data(n, w)
然后,我们来回顾线性回归的求解过程,线性回归的参数w = ( w 0 , w 1 , w 2 , ⋯ , w p ) T \boldsymbol{w} = (w_0, w_1, w_2, \cdots, w_p)^T w = ( w 0 , w 1 , w 2 , ⋯ , w p ) T L ( w ) L(\boldsymbol{w}) L ( w ) 梯度下降算法就是用来求解函数的最小值的算法 ,没错,这里就需要使用梯度下降算法进行求解了,但是在此之前,我们需要先定义损失函数,将损失函数完整写出来为
L ( w ) = ∑ i = 1 n ( y i − y ^ ) 2 = ∑ i = 1 n ( y i − w 0 − w 1 x i 1 − ⋯ − w p x i p ) 2 = ∣ ∣ y − X w ∣ ∣ 2 L(\boldsymbol{w}) = \sum_{i=1}^{n} (y_i - \hat{y})^2 = \sum_{i=1}^{n} (y_i - w_0 - w_1 x_{i1} - \cdots - w_p x_{ip})^2 = ||\boldsymbol{y} - X\boldsymbol{w}||^2
L ( w ) = i = 1 ∑ n ( y i − y ^ ) 2 = i = 1 ∑ n ( y i − w 0 − w 1 x i 1 − ⋯ − w p x i p ) 2 = ∣ ∣ y − X w ∣ ∣ 2
将其翻译为代码就是
1 2 3 4 5 6 7 8 def loss_function (w, X, y ): I = np.ones((np.size(X, 0 ), 1 )) X = np.hstack((I, X)) l = (y - X @ w).T @ (y - X @ w) return l
这里需要注意两个点 ,首先,在写损失函数的时候X X X
X = [ 1 x 11 x 12 … x 1 p 1 x 21 x 22 … x 2 p 1 x 31 x 32 … x 3 p ⋯ 1 x n 1 x n 2 … x n p ] X = \begin{bmatrix}
1&x_{11}&x_{12}&\ldots&x_{1p}\\
1&x_{21}&x_{22}&\ldots&x_{2p}\\
1&x_{31}&x_{32}&\ldots&x_{3p}\\
&&\cdots\\
1&x_{n1}&x_{n2}&\ldots&x_{np}
\end{bmatrix}
X = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 1 1 1 x 1 1 x 2 1 x 3 1 x n 1 x 1 2 x 2 2 x 3 2 ⋯ x n 2 … … … … x 1 p x 2 p x 3 p x n p ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
为了方便计算其增广了一个全1 1 1 X X X 1 1 1
然后,可以看到在代码中我们的写法翻译为数学语言就是L ( w ) = ( y − X w ) T ( y − X w ) L(\boldsymbol{w}) = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) L ( w ) = ( y − X w ) T ( y − X w )
现在我们有了损失函数,但是在梯度下降算法中我们多次需要计算损失函数的梯度,因此我们还需要解决损失函数的梯度的计算问题。幸运的是,这里我们所使用的损失函数是可导的,因此我们可以直接计算出其导数,再将其翻译为代码即可。由于损失函数导数的计算涉及到矩阵求导,这里我们不做过多展开,直接给出计算结果
∂ L ∂ w = X T X w − X T y \frac{\partial L}{\partial \boldsymbol{w}} = X^T X \boldsymbol{w} - X^T \boldsymbol{y}
∂ w ∂ L = X T X w − X T y
将其翻译为代码为
1 2 3 4 5 6 7 8 9 def loss_gradient (w, X, y ): I = np.ones((np.size(X, 0 ), 1 )) X = np.hstack((I, X)) lg = (X.T @ X @ w) - (X.T @ y) lg = lg return lg
完成了准备工作之后,终于可以实现梯度下降了。观察梯度下降全过程,梯度计算我们已经实现并封装好了,还剩下的就是初始化参数 与更新参数 两步了。参数初始化的实现如下
1 w = np.random.randn(np.size(X, 1 )+1 , 1 )
这里还是需要注意两个点 ,首先还是形状问题,“原生”X X X 1 1 1 n × p n \times p n × p w \boldsymbol{w} w w = ( w 0 , w 1 , w 2 , ⋯ , w p ) T \boldsymbol{w} = (w_0, w_1, w_2, \cdots, w_p)^T w = ( w 0 , w 1 , w 2 , ⋯ , w p ) T ( p + 1 ) × 1 (p+1) \times 1 ( p + 1 ) × 1 (np.size(X, 1)+1, 1)。然后是参数初始值一定要随机生成 ,而不是直接给一组整数,例如全0 0 0 1 1 1
然后是参数更新,这个很简单
最后就是套进循环里就可以了,具体实现为
1 2 3 4 5 6 7 8 9 10 def batch_gradient_descent (X, y, alpha, num_iter ): w = np.random.randn(np.size(X, 1 )+1 , 1 ) for i in range (num_iter): lg = loss_gradient(w, X, y) w = w - alpha * lg return w
最后,我还给添加了绘制损失值图像的代码,完整实现为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 def batch_gradient_descent (X, y, alpha, num_iter, loss_plot=True ): w = np.random.randn(np.size(X, 1 )+1 , 1 ) if (loss_plot == True ): L = np.array([loss_function(w, X, y)]) for i in range (num_iter): lg = loss_gradient(w, X, y) w = w - alpha * lg if (loss_plot == True ): L = np.append(L, loss_function(w, X, y)) if (loss_plot == True ): plt.plot(range (num_iter+1 ), L) return w
实现完成,现在用我们自己生成的数据集run一遍看看效果
1 w = batch_gradient_descent(X, y, 1e-3 , 10 )
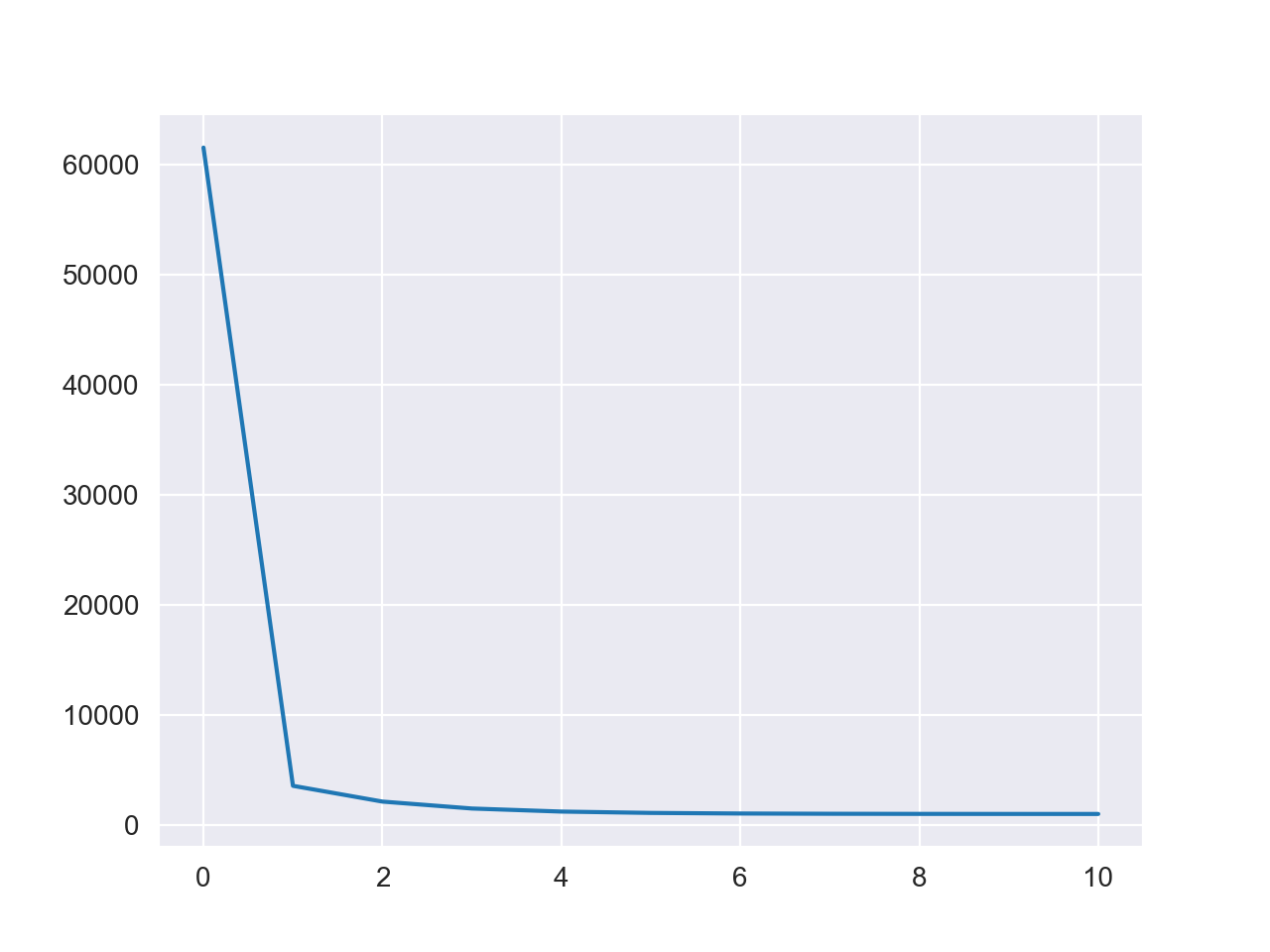
损失值变化图如下
可以看到算法快速完成了收敛,计算结果为
1 2 3 array([[ 8.0084921 ], [ 2.90367565], [-4.02262229]])
基本与原始参数相同,可以视为找到了最优解。
注:此处示范的问题是非常简单的,效果仅限演示,实际操作中,大部分情况下梯度下降当然没有这么简单就找到全局最优解,甚至还会有梯度爆炸或消失等问题。
现在,我们已经了解了梯度下降在深度学习算法中是如何运作的。那让我们把目光聚焦在求解损失函数这个具体的应用上,只针对这一个应用场景,梯度下降存在什么缺点,有没有进一步优化的空间,答案是当然是有的。
首先,让我们来看看我们上面实现的梯度下降,在深度学习中,其被称为批量梯度下降(Batch Gradient Descent) ,因为每一轮迭代都会使用到所有的数据样本。我们来回看线性回归的损失函数
L ( w ) = ∑ i = 1 n ( y i − y ^ ) 2 = ∑ i = 1 n ( y i − w 0 − w 1 x i 1 − ⋯ − w p x i p ) 2 = ∣ ∣ y − X w ∣ ∣ 2 L(\boldsymbol{w}) = \sum_{i=1}^{n} (y_i - \hat{y})^2 = \sum_{i=1}^{n} (y_i - w_0 - w_1 x_{i1} - \cdots - w_p x_{ip})^2 = ||\boldsymbol{y} - X\boldsymbol{w}||^2
L ( w ) = i = 1 ∑ n ( y i − y ^ ) 2 = i = 1 ∑ n ( y i − w 0 − w 1 x i 1 − ⋯ − w p x i p ) 2 = ∣ ∣ y − X w ∣ ∣ 2
很容易可以发现,样本越多损失函数的复杂度越大 ,带来的计算压力也越大。在前面的示例中我们使用的数据集大小在四位数这个数量级,但是在实际工程中常常会有更大数量级的数据集,这对于计算是非常不利的,因此,批量梯度下降在多数时候没有出场空间 。
当然,上述问题的解决思路也很简单。既然每一轮迭代都使用所有数据样本会导致计算压力过大的话,那每一轮迭代都使用部分数据样本不就好了,这也就是深度学习训练中常用的小批量梯度下降(Mini-Batch Gradient Descent) 。
在小批量梯度下降中我们会引入一个新的参数batch_size,其表示每一轮迭代所使用的样本量,例如设定batch_size=10,则每一轮迭代会从数据集中选择10个样本进行梯度下降。不过,如果每次迭代都随机抽取样本的话,那就是等价于对数据集做有放回随机抽样,这种抽样方式有极大概率导致有的样本从头到尾都没有被使用,本着不浪费数据的原则,我们一般会将数据集进行随机打乱,每次迭代都读取一个batch_size大小,直到将数据集完整读完,这个过程被称为一个epoch,在小批量梯度下降中,迭代次数这个参数也自然被epoch所代替。最后,我们给出小批量梯度下降的完整算法流程
输入:特征矩阵X X X y \boldsymbol{y} y α \alpha α epoch,批量大小batch_size
输出:最后一轮的迭代结果w m \boldsymbol{w}_m w m
(1) 随机选取初始值w 0 \boldsymbol{w}_0 w 0 i = 1 i=1 i = 1
(2) 记样本数量为n n n N N N
(3) 从样本编号集N N N batch_size的子集合,记为N b a t c h N_{batch} N b a t c h
(4) 记损失函数$L(\boldsymbol{w}) = \displaystyle \sum_{i \in N_{batch}} (y_i - \hat{y})^2 $
(5) 计算梯度∂ L ∂ w ∣ w = w i − 1 \left. \frac{\partial L}{\partial \boldsymbol{w}} \right|_{\boldsymbol{w}=\boldsymbol{w}_{i-1}} ∂ w ∂ L ∣ ∣ ∣ w = w i − 1
(6) 更新参数w i = w i − 1 − α ∂ L ∂ w ∣ w = w i − 1 \boldsymbol{w}_i = \boldsymbol{w}_{i-1} - \alpha \left. \frac{\partial L}{\partial \boldsymbol{w}} \right|_{\boldsymbol{w}=\boldsymbol{w}_{i-1}} w i = w i − 1 − α ∂ w ∂ L ∣ ∣ ∣ w = w i − 1
(7) 若N N N
(8) 若i = e p o c h i= \mathrm{epoch} i = e p o c h i = i + 1 i = i + 1 i = i + 1
由于指定了每一轮使用的样本数量,因此算法的计算时间可以被控制在一个合理的范围。不过,这会引出下一个问题,就是这种方法会不会对优化效果以及最终收敛结果有影响。那影响肯定是会有的,每一轮迭代只使用部分样本会导致梯度下降多走一些“弯路”,但是,其最终也是可以收敛的。总结一下就是,小批量梯度下降每一轮迭代的时间更短,但是算法收敛所需要的迭代轮次会更多,只要参数设置合理,其计算效率是要高于批量梯度下降的。
最后来到代码实现,从算法流程中我们可以看出这是个两个嵌套循环的算法,外层是循环epoch,内层是每一个epoch迭代的次数
1 2 3 4 5 for i in range (epoch): for j in range (epoch_j):
现在让我们看看,有哪些部分是前面的批量梯度下降中没有实现的。首先是每一个epoch迭代的次数,这里我们记为epoch_j,很自然可以想到data_size除以batch_size,但是我们还要考虑到无法整除的情况。我们上面的例子中的数据集大小为1008,我们设batch_size=10,那在迭代到第100次后,数据集会剩下8个样本,这时候我们采取的策略其实是,使用剩下的8个样本再进行一次迭代,也就是说一共需要迭代101次。我们可以使用数学上的向上取整来准确计算epoch_j,还是用上面的例子,1008/10=100.8,根据我们上面的策略,只要有余数我们就要将其视为1,我们只要在外面套一层向上取整,就可以实现将余数视为1的需求,所以我们就得到了epoch_j的计算公式为
e p o c h _ j = ⌈ d a t a _ s i z e / b a t c h _ s i z e ⌉ \mathrm{epoch\_j} = \lceil \mathrm{data\_size}/\mathrm{batch\_size} \rceil
e p o c h _ j = ⌈ d a t a _ s i z e / b a t c h _ s i z e ⌉
我们可以使用python自带的math库中的math.ceil()函数实现向上取整,因此代码实现为
1 2 import mathepoch_j = math.ceil(data_size/batch_size)
然后是随机生成索引以及读取,这两者是相关的,我们一起讲,实现代码如下
1 2 3 4 5 6 7 8 for i in range (epoch): index = np.random.permutation(data_size) for j in range (epoch_j): index_j = index[j*batch_size : min (j*batch_size+batch_size, data_size)] x_j, y_j = X[index[index_j]], y[index[index_j]] lg = loss_gradient(w, x_j, y_j) w = w - alpha * lg
实现思路是先生成乱序的索引index,然后每一次迭代按顺序取一个batch_size大小,也就是代码中的index_j。例如batch_size=5,那就每一次从乱序索引中取出5个数,这一次取出来的数是[255, 108, 809, 486, 163],那我们就从完整数据集中取出编号为这5个数字的样本,这就是这一次迭代我们要使用的样本,最后的计算梯度与更新参数是没有变化的。
注意这一行代码index_j = index[j*batch_size : min(j*batch_size+batch_size, data_size)],这里的min()函数是用来处理无法整除的情况的。常规情况下都是j*batch_size+batch_size更小,不过在无法整除的情况下,每轮epoch的最后一次迭代中,j*batch_size+batch_size会超过数据集大小,如果没有min()函数处理,这里就会报错。
最后只需要将上述实现封装为函数即可,完整实现为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 def mini_batch_gradient_descent (X, y, alpha, epoch, batch_size=10 , loss_plot=True ): data_size = np.size(X, 0 ) import math epoch_j = math.ceil(data_size/batch_size) w = np.random.randn(np.size(X, 1 )+1 , 1 ) if (loss_plot == True ): L = np.array([loss_function(w, X, y)]) for i in range (epoch): index = np.random.permutation(data_size) for j in range (epoch_j): index_j = index[j*batch_size : min (j*batch_size+batch_size, data_size)] x_j, y_j = X[index[index_j]], y[index[index_j]] lg = loss_gradient(w, x_j, y_j) w = w - alpha * lg if (loss_plot == True ): L = np.append(L, loss_function(w, X, y)) if (loss_plot == True ): plt.plot(range (epoch+1 ), L) return w
同样使用我们生成的数据集run一遍看看效果
1 w = mini_batch_gradient_descent(X, y, 1e-2 , epoch=10 , batch_size=10 )
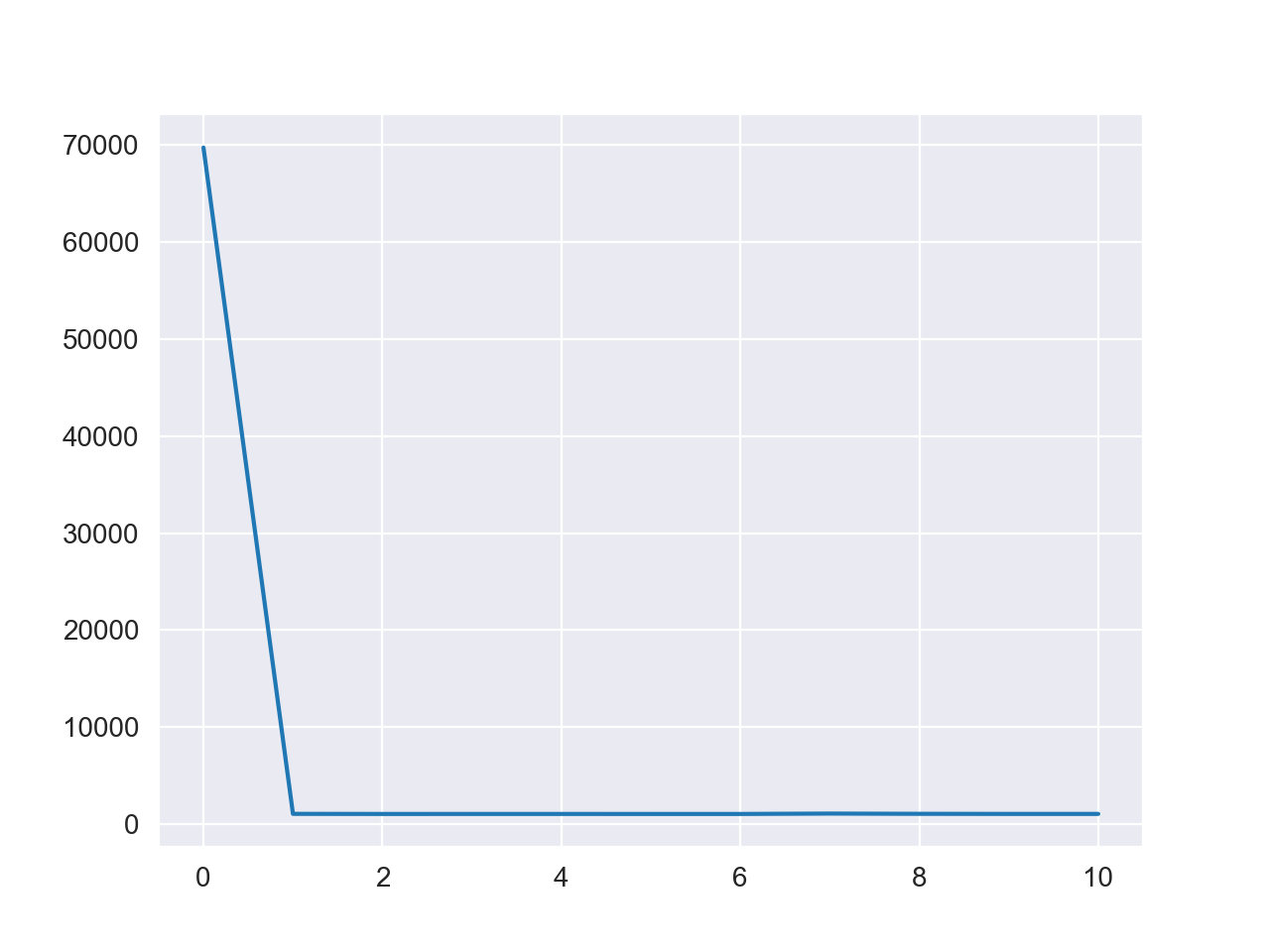
损失值变化图如下
参数计算结果为
1 2 3 array([[ 8.01766359], [ 2.89629187], [-4.00477471]])
最后还有一种常用的变体,就是随机梯度下降(Stochastic Gradient Descent) ,也常常简称为SGD 。随机梯度下降的策略是每一次迭代只使用一个样本计算梯度,其实随机梯度下降就等价于一个批量大小为1的小批量梯度下降 。这是一种更极端的做法,由于每一次迭代只使用一个样本,因此其迭代过程会极其自由,优点是对于复杂的优化问题来说,SGD不容易陷入局部最优解,缺点则是SGD容易不收敛,最后一轮的更新结果不一定就是最优解。也因此,在实际应用中,往往会更倾向于使用更灵活的小批量梯度下降。
SGD的代码实现也非常简单,只需要在小批量梯度下降的基础上修改一些部分即可,完整代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def stochastic_gradient_descent (X, y, alpha, epoch, loss_plot=True ): data_size = np.size(X, 0 ) w = np.random.randn(np.size(X, 1 )+1 , 1 ) if (loss_plot == True ): L = np.array([loss_function(w, X, y)]) for i in range (epoch): index = np.random.permutation(data_size) for j in range (data_size): x_j, y_j = X[index[i], None ], y[index[i], None ] lg = loss_gradient(w, x_j, y_j) w = w - alpha * lg if (loss_plot == True ): L = np.append(L, loss_function(w, X, y)) if (loss_plot == True ): plt.plot(range (epoch+1 ), L) return w
首先,epoch_j在随机梯度下降中其实就是data_size,所以也不需要算epoch_j了。然后是这部分代码X[index[i], None],这里依旧是numpy的老问题。如果我们运行X[0].shape,会发现输出为(2,),numpy删维度了,而None的作用就是手动增加一个维度,如果运行X[0, None].shape就会发现输出为(1, 2),这就是我们希望的正确维度信息。
1 w = stochastic_gradient_descent(X, y, 1e-2 , 10 )
运行结果如下图
可以看到相比于前面两种算法,SGD的随机性明显更强,中间甚至出现了损失值上升的情况。这也提示我们,在使用小批量梯度下降时,使用较小的batch_size可以增加算法迭代的随机性,反正亦然。
回顾一下三种梯度下降算法,不难发现,批量梯度下降与随机梯度下降都是小批量梯度下降算法的一种特例 。所以我们不难考虑到,实现一个统一的函数用于三种梯度下降算法,这里我参考了沐神的《动手学深度学习》 中的代码写法。
首先,我们需要将读取一个batch这部分封装为一个函数,代码如下
1 2 3 4 5 6 7 8 9 10 11 12 def data_iter (batch_size, features, labels ): data_size = np.size(features, 0 ) index = np.random.permutation(data_size) for i in range (0 , data_size, batch_size): batch_index = index[i: min (i + batch_size, data_size)] X, y = features[batch_index], labels[batch_index] X, y = X.reshape(np.size(batch_index), -1 ), y.reshape(np.size(batch_index), -1 ) yield X, y
划分batch的思路与上面的所讲的并无二致,关键之处在于我们使用了yield关键字,这部分涉及python的迭代器与生成器 相关的知识,对此不了解的读者可以移步Python:迭代器与生成器 。
使用上述的实现的data_iter()函数配合for循环,我们只需要给定batch_size就可以实现batch的读取,循环内只需要写计算梯度跟更新参数,外层再套一个epoch的循环,一个梯度下降的过程就完成了,具体代码为
1 2 3 4 for epoch in range (epochs_num): for X, y in data_iter(batch_size=batch_size, features=features, labels=labels): gradient = loss_gradient(w, X, y) w = w - alpha * gradient
将更新参数部分进行独立封装(为方便后续改进),并且将上述训练过程也进行封装,可以得到完整代码为
1 2 3 4 5 def gradient_descent (w, gradient, alpha ): w = w - alpha * gradient return w
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def LR_train (features, labels, epochs_num, batch_size=10 , alpha=0.0001 ): w = np.random.randn(np.size(features, 1 )+1 , 1 ) for epoch in range (epochs_num): for X, y in data_iter(batch_size=batch_size, features=features, labels=labels): gradient = loss_gradient(w, X, y) w = gradient_descent(w, gradient, alpha) train_l = loss_function(w, features, labels) print (f'epoch {epoch + 1 } , loss {float (train_l):f} ' ) return w
1 w = LR_train(X, y, epochs_num=10 , batch_size=10 , alpha=0.05 )
设置参数并使用生成数据集进行训练,结果如下
1 2 3 4 5 6 7 8 9 10 epoch 1, loss 1031.024954 epoch 2, loss 1076.142810 epoch 3, loss 1043.372326 epoch 4, loss 1040.924981 epoch 5, loss 1030.162326 epoch 6, loss 1079.752369 epoch 7, loss 1048.653924 epoch 8, loss 1052.039613 epoch 9, loss 1029.410970 epoch 10, loss 1029.873922
对于我们改进后的代码,只需要设置batch_size=1即可以使用随机梯度下降,设置batch_size=data_size则可以使用批量梯度下降,其余设置则均为使用小批量梯度下降。
本文介绍了梯度下降算法的作用与原理,并结合线性回归与代码,细致介绍了梯度下降算法在深度学习中发挥的作用,最后结合深度学习训练中所遇到的问题,介绍了梯度下降在深度学习中常用的几种变体。